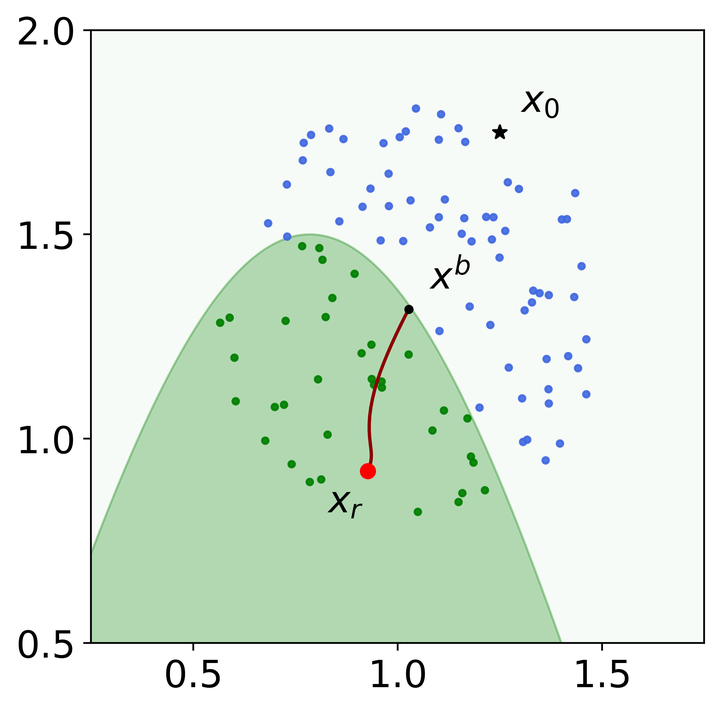
Visualization of the isotropic Gaussian (dashed, opaque), the worst-case distributions (solid) around each sample, and the optimization trajectory of the recourse.Abstract
Algorithmic recourse aims to recommend an informative feedback to overturn an unfavorable machine learning decision. We introduce in this paper the Bayesian recourse, a model-agnostic recourse that minimizes the posterior probability odds ratio. Further, we present its min-max robust counterpart with the goal of hedging against future changes in the machine learning model parameters. The robust counterpart explicitly takes into account possible perturbations of the data in a Gaussian mixture ambiguity set prescribed using the optimal transport (Wasserstein) distance. We show that the resulting worst-case objective function can be decomposed into solving a series of two-dimensional optimization subproblems, and the min-max recourse finding problem is thus amenable to a gradient descent algorithm. Contrary to existing methods for generating robust recourses, the robust Bayesian recourse does not require a linear approximation step. The numerical experiment demonstrates the effectiveness of our proposed robust Bayesian recourse facing model shifts. Our code is available at https://github.com/VinAIResearch/robust-bayesian-recourse.
We introduce a model-agnostic recourse that minimizes the posterior probability odds ratio along its min-max robust counterpart with the goal of hedging against future changes in the machine learning model parameters. Robust Bayesian Recourse explicitly takes into account possible perturbations of the data in a Gaussian mixture ambiguity set prescribed using the optimal transport (Wasserstein) distance.
